Аналого-цифровые и цифро-аналоговые преобразователи

Неисчерпаемый аналоговый мир

Любая деятельность человека так или иначе связана с получением и обработкой информации. Британская Энциклопедия сообщает: "Люди воспринимают информацию органами чувств: звуки - слухом; изображения и текст - зрением; форму, температуру и воздействия (affection) - осязанием; запахи - обонянием. Чтобы интерпретировать сигналы, принятые органами чувств, люди разработали и освоили сложные системы языков, состоящих из алфавитов (символов) и стимулов (раздражителей), и правил их употребления. Это позволило узнавать увиденные предметы, понимать прочтенные или услышанные сообщения и постигать смысл знаков, воспринятых осязанием и обонянием".

Однако одни объекты и явления окружающего мира воспринимаются и осмысливаются нами как некие целостные отдельные, "дискретные" сущности (discretus по латыни - разделенный, отдельный, прерывистый), другие же представляют собой непрерывные процессы, развивающиеся во времени (continuum - непрерывный, продолжающийся). Однако, как замечает энциклопедия, основным инструментом для интерпретации входящей информации в обоих случаях являются "алфавиты", то есть наборы отдельных объектов. Наш разум более склонен манипулировать дискретными объектами, нежели непрерывными процессами, этим и обусловлено развитие дискретных технологий.

Познанию закономерностей физических процессов неизменно предшествует стадия накопления данных - результатов измерений характеристик этих процессов. Для представления и хранения этих результатов, как известно, используются числа. Но здесь есть одна проблема. Использование чисел для пересчета целостных, "штучных" объектов особых трудностей не вызывает, для этого используются натуральные числа.

А вот с измерениями  несколько сложнее. Измерить - значит сопоставить реальную величину с неким эталоном, а природа вещей такова, что величины не хотят быть кратными какому-то эталону, они существуют в пространстве действительных чисел, а действительные числа обладают важным свойством: как близко бы мы не выбрали два числа на отрезке числовой оси, между ними обязательно отыщется место хотя бы для еще одного.

Это свойство вещественных чисел называется плотностью. Любой измерительный инструмент, от линейки до электронного микроскопа, имеет пусть и большое, но ограниченное разрешение. Даже если бы у приборов было неограниченное разрешение, оставалась бы проблема записи результатов, так как действительное число записывается бесконечной последовательностью десятичных цифр. Увы, нам доступны лишь ограниченные наборы знаков, независимо от того, какой физический носитель служит хранилищем информации.

Из вышесказанного следуют два вывода.

1. Измерения реальных физических величин неизбежно сводятся к упрощению, "прореживанию" реальности: мы делаем выборку в отдельные моменты времени и отображаем результат с помощью ограниченного набора значений (рис 1.).

Рис 1

Можно, конечно, фиксировать ход физического процесса, скажем, на бумажной ленте с помощью самописца, но этот результат равнозначен самому исходному процессу: как только мы попытаемся анализировать, придется заняться измерениями уже на самой этой ленте, и мы в итоге придем к тому же самому.

2. Процесс перехода от реальных величин или характеристик реальных процессов к неким конечным наборам элементов, составляющий суть аналого-цифрового преобразования, был известен человечеству со времен зарождения математики. Поэтому ничего принципиально нового или мистического приборы, называемые аналого-цифровыми и цифро-аналоговыми преобразователями (АЦП и ЦАП), не делают, а просто автоматизируют некую работу.

Приближенный или упрощенный характер измерений не так уж страшен. Мы, в принципе, можем увеличивать их точность настолько, насколько это необходимо для решения конкретных задач.

И о терминологии. Вообще говоря, термины "аналоговый" и "дискретный" принято относить к радиотехнике: если сигнал порожден физическим процессом, который можно описать непрерывной функцией, то его называют аналоговым, имея в виду его соответствие реальному процессу. Дискретный сигнал, как правило, является последовательностью импульсов, применяемых для кодирования чисел. Чаще всего речь идет о двоичном представлении чисел. В этом случае единица представлена высоким, а нуль - низким потенциалом напряжения (рис.2).

Рис 2

Однако, термин "аналоговый" часто используют шире, имея в виду "нецифровой", "некомпьютерный", и т.д. Например, с появлением цифровой фотографии фотографию на основе фотохимических процессов, с фотопленкой и проявкой, тоже стали называть "аналоговой".

Теорема отсчетов

Представим себе, что нам нужно оцифровать аналоговый сигнал, амплитуда которого задана непрерывной функцией времени u(t) (рис.1а). Категория непрерывности в математике выражается определенной формулой, но и представления на уровне здравого смысла будет достаточно. Как мы помним, "упрощение реальности" идет и по оси t (выборка есть счетное множество), и по оси u (ограничения, накладываемые разрядностью чисел, используемых для записи результатов) (рис.1б). Переход от непрерывного сигнала к множеству выборок его значений в определенные моменты времени (t₀, t₁, t₂ ,...) называется дискретизацией, а количественное представление амплитуды в соответствии с заданной разрядностью - квантованием. (Используемое иногда слово "семплирование" означает совокупность дискретизации и квантования – прим. ред.) Дискретизацию можно сравнить с киносъемкой, где непрерывное движение фиксируется конечным числом кадров в единицу времени.

Забудем на время о квантовании (будем считать, что выборки соответствуют точным значениям u(tn)) и попробуем решить, насколько часто нужно делать выборки, то есть какова должна быть частота дискретизации, если мы хотим впоследствии по отсчетам восстановить исходный сигнал. На рисунках 3 и 4 показаны попытки дискретизации синусоидального сигнала, красные точки соответствуют дискретным значениям - отсчетам (семплам).

Рис 3

Рис 4

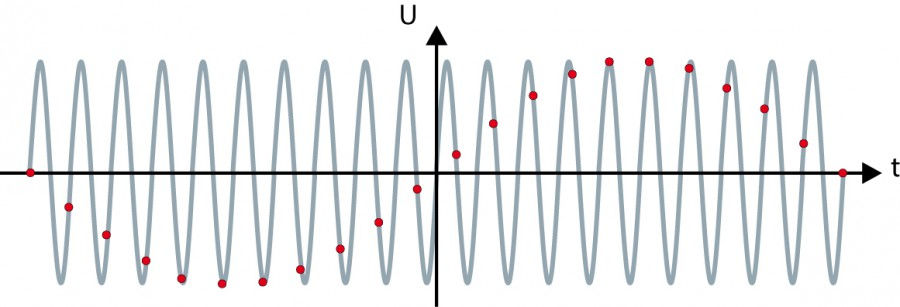
Частота исходного сигнала на рис. 3 составляет 0,09 от частоты дискретизации. Результат можно считать приемлемым, так как, соединив соседние точки, получим кривую, близкую к форме исходного сигнала. А вот про случай на рис. 4 этого не скажешь. Здесь частота сигнала близка к частоте дискретизации (0,95), и в результате отсчеты выстраиваются в синусоиду, только совсем другую, с частотой раз в двадцать меньше. Нечто подобное можно иногда наблюдать в кино, когда колеса у машины вдруг начинают крутиться в обратную сторону.

Феномен изменения частоты синусоиды в результате дискретизации называется aliasing (alias по-английски - псевдоним). О восстановлении исходного сигнала говорить уже не приходится.

Интуитивно понятно, что чем чаще делаются выборки, тем точнее мы отобразим характер изменения функции, однако увеличивать частоту дискретизации до бесконечности мы не можем, и нам нужен критерий, где остановиться. Он существует в лице знаменитой теоремы отсчетов, имеющей и другие названия: в России - теорема Котельникова, в остальном мире - теорема Найквиста (Nyquist), являющаяся частным вариантом более общей теоремы Шеннона (Shannon).

Обычно ее формулируют так: "Произвольный сигнал u(t), спектр которого ограничен некоторой частотой F_B, может быть полностью восстановлен по последовательности своих отсчетов, следующих с интервалом времени ∆t = 1/(2 F_B)". То есть частота дискретизации должна как минимум вдвое превышать максимальную частоту, присутствующую в спектре сигнала, и тогда все будет нормально. Однако внимательного читателя могут насторожить слова "может быть полностью восстановлен". О том, каким образом сигнал будет восстанавливаться, многие источники скромно умалчивают. Ведь через набор точек на плоскости, соответствующих отсчетам, можно провести бесчисленное множество кривых! (рис.5)

Рис 5

Вот она, эта великая формула:

Формула

Здесь k - номер отсчета; произведение k∆t - момент времени, соответствующий k-му отсчету; u(k∆t) - само значение k отсчета, и ωB = 2пF_B = п/∆t - максимальная (верхняя) частота спектра, только выраженная в радианах. Часто величину ∆t называют шагом (интервалом) дискретизации, а FB - частотой Найквиста.

В некоторых источниках частотой Найквиста называют величину, равную 2F_B, то есть частоту дискретизации! Это, вообще говоря, непринципиально, но, во избежание путаницы, еще раз подчеркнем: здесь под частотой Найквиста F_B мы будем подразумевать половину частоты дискретизации.

Таким образом, достаточно располагать частой выборкой значений u(k∆t), и исходная функция (сигнал) восстанавливается полностью, ибо равенство в формуле не приближенное, а строгое. Однако если быть абсолютно точными, равенство справедливо в случае, если мы, скажем, оцифровываем музыкальное произведение, длящееся с Начала Времен (тут мы уже опоздали), и которое никогда не кончится. Если же рассматривать ограниченный отрезок времени, то бесконечной сумма может стать, если ∆t будет бесконечно малой величиной. Раз уж мы подступаемся к бесконечности (непрерывности) с ограниченными выборками, придется забыть о строгих равенствах.

И, тем не менее, переходя к практике, можно убедиться, что и теорема, и формула действительно работают. Попробуем разобраться, как это происходит. Во-первых, выражение,

sinω_B(t - k∆t)/ω_B( - k∆t) (2)

 на которое умножается значение отсчета в формуле (1), является функцией вида sin x/x, сжатой вдоль горизонтальной оси в ω_B раз (рис. 6).

Рис 6

Это так называемая функция Котельникова (базисная функция, функция отсчетов). То, что x здесь равно не ω_B × t, а ω_B × (t- k∆t), приводит к тому, что график сдвигается влево на k∆t. В итоге получается "частокол" из функций с вершинами в точках, соответствующих значению отсчетов u(k∆t), так как максимум любого сомножителя (2) есть единица. Этот частокол и надо просуммировать. Вот результаты небольшой лабораторной работы на эту тему (рис.7).

Рис 7

В качестве шага дискретизации было выбрано число 1 (следовательно, ω_B =п), и всего три отсчета: u(0) = 1,2 (коричневая кривая на рисунке), u(1) = 1,4 (зеленая) и u(2) = 1,6 (синяя). Таким образом, слагаемых было не бесконечное число, а всего три, и, тем не менее, результат получился довольно убедительный: суммирующая кривая красного цвета проходит через все три точки, плавно соединяя их, и быстро сходит на нет справа и слева (рис. 7 и 8).

Рис 8

Общее же свойство таково: при любом произвольном количестве слагаемых результирующая кривая точно проходит через выбранные точки отсчетов, а в промежутках между ними сколь угодно близко приближается к исходному сигналу (по мере роста числа слагаемых). Все вышесказанное не означает, разумеется, что цифро-аналоговые преобразователи обязательно восстанавливают исходный сигнал по значениям отсчетов именно таким образом. Но важно то, что "правильное" восстановление в принципе существует.

Квантование

Следующим ключевым моментом является цифровое представление значений отсчетов ("прореживание" вертикальной оси u) - квантование. Реальные значения должны быть представлены в виде N-разрядного двоичного числа. Такое число может принимать 2^N различных значений. Например, для 16-битных чисел N=16, а 2^N = 65536. Вот на столько долей надо разбить вертикальную ось, а после решать, в какой отрезок попадает то или иное значение отсчета. Совершенно очевидно, что чем больше разрядов в числе, тем более точной и полной будет кодируемая информация.

Мы сравнивали дискретизацию сигнала с киносъемкой, когда непрерывное движение представляется в виде череды кадров, и частота дискретизации аналогична частоте смены кадров. Если продолжить эту аналогию, то разрядность числа при квантовании можно соотнести с размером кадра. Ширина киноленты может варьироваться от 8 до 70 мм. Ясно, что кадр большего размера способен нести больше информации. Можно для иллюстрации привести еще такой пример. Представим, что нам нужно измерить высоту дерева, а мы располагаем лишь шестом с метровыми отметками. Тогда придется считать, что высота дерева равна, скажем, 3 или 4 метрам, а то, что в действительности его длина составляет 3м 75 см, знать нам будет не дано.

Добавляя двоичному числу новый разряд, мы увеличиваем диапазон принимаемых им значений вдвое. Для амплитуды звукового сигнала, каковой и является наша функция u(t), это равносильно расширению динамического диапазона на 6 дБ. Таким образом, динамический диапазон цифрового звука прямо пропорционален разрядности числового (двоичного) представления отсчетов. Для 16-битных систем это будет величиной порядка 96 дБ, а для 24-битных - 144 дБ.

Рассмотренное здесь квантование относится к линейному типу, то есть весь диапазон изменения амплитуды сигнала делится на равные промежутки величиной 1/2^N (шаг квантования ∆ на рис. 9а).

Известны также примеры других, нелинейных моделей, когда разрядность переменна и зависит от амплитуды.

Рис 9

Проблемы и их решения

В силу вышесказанного оцифрованный сигнал будет иметь вид лесенки (рис. 9а). Математически это будет означать, что мы имеем дело с суммой двух сигналов - исходного и некоего дополнительного зигзагообразного (рис. 9б). Последний называется шумом квантования, и служит источником искажений.

Борьба с этим явлением происходит по принципу "лечить подобное подобным". Во входной сигнал подмешивается белый шум. Таким образом, нарушается неприятная для нас регулярность шума квантования. Этот феномен можно проиллюстрировать так. Если перед нами находится неподвижное колесо, то объект, находящийся за ним, не удается рассмотреть как следует - мешают спицы. При быстром вращении спицы сливаются в серый, практически прозрачный круг. Сами спицы при этом никуда не деваются, но перестают быть помехой для наблюдателя.

Добавочный белый шум называется по-английски dither (дрожь). Сам процесс называется dithering. Из рисунка видно, что амплитуда шума квантования по абсолютной величине не превосходит ∆. Величина ∆= 1/2^N соответствует младшему разряду N-битного числа, поэтому нужно обеспечить появление в этом разряде случайной величины, которая разрушит устойчивую форму шума квантования. Это и достигают, применяя dithering.

Dithering считается "неизбежным злом" в цифровой технике. Увеличивая общий уровень шума, он, тем не менее, обязательно присутствует практически в любом современном АЦП, независимо от того, заявлено это в документации или нет. (Там, где он отсутствует, это заметно по неудовлетворительному качеству звучания). Кроме АЦП, dithering зачастую применяется в других цифровых процессорах - эквалайзерах, компрессорах и пр.

Другой серьезной проблемой является aliasing, о котором уже упоминалось выше. Это явление возникает при попытке оцифровать сигнал, частота которого превышает частоту Найквиста. Допустим, мы снимаем на ленту периодически вспыхивающую лампу, постепенно увеличивая частоту вспышек. В какой-то момент частота вспышек будет равна половине частоты смены кадров. В этот период на ленте будут чередоваться кадры со светом и темнотой, что нормально. Если же частота вспышек сравняется с частотой кадров, то на ленте или везде будет свет, или везде темнота, в зависимости от того, на какую фазу мы попадем. Съемка, таким образом, становится бессмысленной.

Если мы выбираем частоту дискретизации 44,1 кГц, то считаем, что она должна обеспечить предел слышимых частот, равный 20 кГц, а что дальше - не имеет значения. А вот и имеет! Если в сигнале, который мы, в соответствии с теоремой отсчетов, оцифровываем с частотой 2F_B, обнаруживается составляющая, имеющая частоту F_H > F_B, то после оцифровки она будет иметь другую частоту: F_HD = 2F_B - F_H, попадая в область слышимых частот (рис.10)!

Рис 10

Ясно, что запись будет непоправимо испорчена. На графике амплитудно-частотной характеристики вертикальная линия, соответствующая F_B, выполняет роль зеркала, отражая при оцифровке высокочастотные составляющие в левую по отношению к себе область графика. А такие высокочастотные паразитные составляющие в исходном сигнале обязательно будут присутствовать. Поэтому перед аналого-цифровым преобразованием сигнал необходимо пропустить через фильтр низких частот (ФНЧ). Но подробнее об этом поговорим ниже, а пока сформулируем еще одну проблему.

Полученный в результате аналого-цифрового преобразования дискретный сигнал является последовательностью прямоугольных импульсов. Из теории преобразований Фурье хорошо известно, что прямоугольный импульс (как, впрочем, импульс любой формы) может быть аппроксимирован, то есть представлен в виде суммы синусоидальных сигналов с соответствующими коэффициентами. Так что спектр простой периодической последовательности прямоугольных импульсов имеет довольно затейливый характер (рис. 11а).

Рис 11

А если к тому же эта последовательность несет в двоичном виде информацию об исходном аналоговом сигнале u(t), который также имеет спектр определенного вида (рис.11б), то для нас не должно быть неожиданностью то, что окончательный спектр дискретного сигнала, как результата аналого-цифрового преобразования, представляет из себя столь пышный "букет" (рис 11в) периодической структуры. Проблема в том, что нужно выделить только центральный "лепесток", отбросив остальные. Как и в предыдущем случае, это можно сделать с помощью ФНЧ. Но здесь начинаются настоящие трудности. Фильтр и в том, и в другом случае должен иметь высокий порядок, не ниже 12-го. Создание таких фильтров вызывает значительные технические сложности, а, кроме того, фильтры высокого порядка вносят заметные фазовые искажения. Возможно, именно из-за неудач в этой области у многих надолго закрепилось отрицательное отношение к цифровому аудио.

Один из путей решения проблемы состоит в увеличении частоты дискретизации в несколько раз. Этот метод носит название oversampling или передискретизации. При аналого-цифровом преобразовании применяется аналоговая передискретизация, то есть выборка отсчетов делается на повышенной частоте. Другая разновидность - цифровая передискретизация, используется при цифро-аналоговом преобразовании. Это искусственное увеличение частоты дискретизации. Между соседними отсчетами вставляются несколько "фиктивных" нулевых отсчетов, и результат затем обрабатывается специальным цифровым фильтром, что позволяет "восстановить" (интерполировать) эти новые значения так, как если бы они были реальными. Применимы и более традиционные методы, когда для интерполяции используются различные вычислительные алгоритмы. В результате частота дискретизации увеличивается в несколько раз, что качественным образом меняет картину: становится допустимым применение аналоговых ФНЧ рядовых характеристик, что существенно упрощает технические решения АЦП и ЦАП.

Принципы работы АЦП и ЦАП

ЦАП (в англоязычной литературе DAC, Digital-to-Audio Converter) является более простым устройством, чем АЦП (ADC, Audio-to-Digital Converter), и даже часто служит одним из элементов последнего. Рассмотрим простейший четырехразрядный ЦАП, основанный на суммировании напряжений, соответствующих разрядам двоичного числа (рис.12).

Рис 12

Резистивная матрица состоит из четырех сопротивлений, каждое из которых соответствует своему двоичному разряду, причем номинал сопротивления обратно пропорционален значимости разряда. Сопротивления соединены с инвертирующим входом операционного усилителя с помощью ключей, которые управляются двоичным кодом, поступающим на вход ЦАП (Q_i равно единице - ключ замкнут, равно нулю - разомкнут). Определим амплитудное значение, соответствующее младшему разряду двоичного числа (уровню квантования) ∆ = -ER₀ /R, где E - постоянное напряжение. Тогда на выходе ЦАП образуется напряжение: uвых = ∆(Q₀ + 2Q₁ + 4Q₂ + 8Q₃).

В соответствии с двоичным кодом выходное напряжение может меняться от 0 до 15∆, изменение происходит скачкообразно и может быть сглажено ФНЧ. При увеличении числа разрядов величина сопротивления, соответствующего младшему разряду, растет в геометрической прогрессии, к тому же в этой схеме от резисторов требуется высокая точность и стабильность, а этого добиться в интегральном исполнении весьма проблематично. Считается, что такая схема пригодна для устройств низкой разрядности.

Другая схема относится к типу R-2R. Это уже вполне рабочая модель, имеющая широкое распространение (например, Burr Brown PCM61, PCM63, PCM1702). Здесь входное сопротивление матрицы постоянно равно R, а 2R-резисторы подключаются в зависимости от значения двоичного разряда либо к нулевой точке, либо к инвертирующему входу операционного усилителя (рис. 13).

Рис 13

Выходное напряжение здесь: u_вых = (∆/2³)(Q₀ + 2Q₁ + 4Q₂ + 8Q₃).

Высокая разрядность и интегральное исполнение для этой схемы вполне допустимы.

Рассмотрим теперь несколько принципиальных схем АЦП - последовательную, параллельную и последовательно-параллельную.

Рис 14

В основе последовательной схемы (рис. 14) лежит счетчик тактовых импульсов Ст, поступающих от генератора М через логический элемент & (И), второй вход которого управляется RS-триггером Т. Специальный стартовый импульс устанавливает вход S (set) триггера в состояние "1", тогда выход триггера тоже переключается в состояние "1", что позволяет тактовым импульсам проходить через логический элемент & на вход счетчика Ст, где и происходит их суммирование. Значения выходных разрядов счетчика преобразуются ЦАПом в напряжение, поступающее на вход компаратора К. Там оно сравнивается с величиной входного сигнала u_вх, и как только эти величины совпадут, компаратор К посылает на вход триггера R (reset) сигнал, обнуляющий выход триггера. Таким образом, поступление тактовых импульсов через & прекращается, и мы получаем наше четырехразрядное число. Очевидно, что данная схема не является быстродействующей.

В этом смысле более выигрышна схема параллельного АЦП (рис. 15).

Рис 15

Здесь используются несколько компараторов, на неинвертирующие входы которых подается входной сигнал u_вх. На инвертирующий вход каждого компаратора с помощью резистивного делителя подается свое опорное напряжение так, чтобы разность опорных напряжений двух соседних компараторов составляла шаг квантования ∆. Таким образом, происходит одновременное сравнение величины входного сигнала с разными опорными напряжениями, и, в случае превышения входным напряжением опорного компаратор, выдает "1" на соответствующий вход шифратора. Шифратор имеет m входов, пронумерованных десятичными числами и n выходов, соответствующих двоичным разрядам. Поступившая на один из входов шифратора единица вызывает появление на выходе двоичного кода, соответствующего этому входу. Последовательные схемы отличаются быстродействием, но требуют большого числа компараторов.

Компромиссом между скоростью и количеством элементов являются последовательно-параллельные схемы. Возможна схема из одного ЦАП и двух АЦП: первый выделяет из входного сигнала старшие разряды, которые затем опять преобразуются ЦАПом в аналоговый сигнал, который вычитается из сигнала исходного, и полученная таким образом разность попадает на вход второго АЦП, который и вычисляет оставшиеся младшие разряды.

Существуют и другие принципы построения АЦП. Так, например, метод двухэтапного интегрирования основан на измерении времени зарядки емкости входным напряжением u_вх и последующей ее разрядки током обратной полярности.

Особое место занимают АЦП и ЦАП на основе сигма-дельта модуляции (Σ∆). Метод заключается в дискретизации на очень больших частотах, превышающих частоту Найквиста в десятки раз. Для квантования при этом достаточно всего одного разряда (бита), и храниться в нем будет уже не амплитуда сигнала, а признак ее изменения ("дельта"): возрастание амплитуды кодируется 1, уменьшение - 0, а отсутствие изменения - чередованием нулей и единиц. При этом сумма значений на участке t, соответствующему дискретизации с частотой 2F_B, пропорциональна значению обычного отсчета. Низкоразрядное квантование сопровождается шумом высокого уровня, к которому путем применения рекурсивного фильтра применяют преобразование, известное под названием noise shaping, в результате которого преобразуется спектр шума: уровень шума понижается для частот, меньших F_B (то есть в слышимой полосе спектра), и повышается в области высоких частот. После этого однобитный поток направляется на фильтр-дециматор, где преобразуется в обычную последовательность отсчетов. Цифро-аналоговое преобразование проходит все стадии в обратном порядке, причем начинается с фильтра-интерполятора, где происходит значительная передискретизация и вычисление промежуточных значений отсчетов. К числу достоинств метода сигма-дельта можно отнести простоту построения преобразователей и способность ЦАП обеспечить более высокую эффективную разрядность по сравнению с входным сигналом, то есть сделать звучание более сглаженным и комфортным.

Джиттер

Эта проблема не затрагивалась выше, так как непосредственно к технологиям цифро-аналоговых и аналого-цифровых преобразований отношения как бы не имеет. Однако если речь заходит о работе с конкретными устройствами, эту тему обойти стороной нельзя.

Итак, джиттер (jitter) - злейший враг цифровых систем. Ибо все то, о чем здесь шла речь - дискретизация, квантование, восстановление сигнала, спектральные характеристики и т.д. - основывается на том простом предположении, что отсчеты следуют друг за другом через равные промежутки времени. Любые реальные цифровые системы работают сообразно с сигналами, которые постоянно вырабатывает их внутренний генератор тактовой частоты (clock). Продуцируя через равные промежутки времени синхросигналы прямоугольной формы, он является для системы высшей инстанцией во всем, что касается вопросов времени.

Джиттер определяется как нарушение регулярности синхросигналов (их также называют тактовыми импульсами). Обычно это проявляется в быстром дрожании фазы сигнала вследствие смещения импульса во времени, или нарушении его формы. В случае аналого-цифровых преобразований именно тактовыми импульсами определяется момент, в который мы получаем значение каждого отсчета, поэтому от качества синхросигнала впрямую зависит качество отображения аналогового сигнала. Продолжая аналогию с киносъемкой, джиттер можно сравнить с неравномерно работающим лентопротяжным механизмом камеры. Если мы снимаем ровный бег лошади, которая в каждом кадре должна перемещаться на одинаковое расстояние, можно себе представить, что мы увидим, если при съемке кадры чередовались с задержками разной величины!

Как джиттер воспринимается слухом? Главным образом это приводит к неточной передаче или даже к искажению тембра, также это явление воздействует на субъективно воспринимаемое пространственное расположение источников звука и способно привести слушателя к некоторой дезориентации, а иногда даже вызвать ощущение, будто запись прокручивают назад.

Причины возникновения джиттера могут быть различными - от сильных электромагнитных влияний до некачественного оборудования или неправильно подобранных соединительных кабелей. Один из самых критических моментов здесь - передача цифровых данных от одного устройства к другому. Например, в форматах AES/EBU или SP/DIF, где данные передаются 32-битными кадрами, синхронизирующие биты присутствуют в каждом кадре. Однако эта информация может быть надежно воспринята и распознана только тогда, когда тактовые импульсы в приемном устройстве синхронизированы с тактовыми импульсами передатчика. Если это сделано некачественно или вовсе не сделано, тогда - вот он, джиттер. Поэтому если устройство имеет возможность работы с внешней синхронизацией, ею обязательно надо пользоваться.

Часто рекомендуют асинхронные двунаправленные интерфейсы. Нелишне будет позаботиться о качестве соединительных кабелей, хотя бы о соответствии их стандартам. Если есть возможность выбрать цифровой интерфейс, можно вспомнить, например, что оптические системы не подвержены электромагнитным помехам, а симметричные AES/EBU неплохо от них защищены. В плане оборудования есть смысл обратить внимание на тех производителей, которые затрачивают значительные усилия на разработку соответствующих решений.

Полезные советы

Напоследок еще несколько соображений практического характера. Высококачественный прибор не всегда автоматически соответствует высокой цене. А аналого-цифровые или цифро-аналоговые преобразователи - сложные конструкции, и создать их непросто. Поэтому при покупке изучать их надо внимательно.

Вот, например, схемотехника. Любой пробразователь, помимо цифровой части, как-то спроектирован и в своей аналоговой части. То, что разъем XLR предпочтительнее мини-джека, объяснять никому не надо. А вот то, что из-за собственных шумов аналого-цифровой преобразователь теряет часть своего цифрового разрешения, возможно, не всем известно. А ведь три децибела собственных шумов - и один бит долой! Заявленные теоретические параметры чипов - это еще не сама реальность. Часто думают, что качество прибора определяется качеством комплектующих, но это не совсем верно. Гораздо важнее его схемотехника и то, как из этих комплектующих прибор собран. Будьте внимательны и не ошибитесь при выборе!